Pythonで音声解析 – 音声データの周波数特性を調べる方法

イヤホンをしていると家のチャイムが鳴ったことに気づかないことがあるのと、外出中に来客があったかどうかを調べるために、家のインターホンの音声データを認識させ、チャイムが鳴ったら自分にLINEを飛ばすプログラムを作成しました。

この記事では、そのような音声処理プログラムを作成する際に必要となる、Pythonを用いた音声解析の基本的な方法について紹介します。

Pythonによるデータ分析入門 第2版

　　　　

Python実践データ分析100本ノック

　　　

　　　　

今回やること

• 音声データをグラフ表示
• 周波数成分を取得
• スペクトログラムにより、いつどんな周波数が含まれているか表示

　　　　

実行環境

・Windows 10
・Python 3.7

※python3.9では正しく動作しないとの報告を頂きました。(2021/5現在)

　　

準備

まず最初に、必要なモジュールをインストールします。

pip install numpy
pip install librosa
pip install matplotlib
pip install scipy 

次に、解析する音声ファイル（wav）を用意します。

今回はインターホンのチャイムの音を解析しました。

解析に使用したインターホンの音声データは↓これです。

　　

音声データを表示

まず最初に音声データの中身をそのまま表示してみます。

import sys
import scipy.io.wavfile
import numpy as np
import matplotlib.pyplot as plt


#音声ファイル読み込み
args = sys.argv
wav_filename = args[1]
rate, data = scipy.io.wavfile.read(wav_filename)

##### 音声データをそのまま表示する #####
#縦軸（振幅）の配列を作成   #16bitの音声ファイルのデータを-1から1に正規化
data = data / 32768
#横軸（時間）の配列を作成　　#np.arange(初項, 等差数列の終点, 等差)
time = np.arange(0, data.shape[0]/rate, 1/rate)  
#データプロット
plt.plot(time, data)
plt.show()

rateは一秒間にサンプリングされる回数（サンプリング周波数）
dataはサンプリング時の振幅（音量）です。

上記のプログラム実行時に音声ファイルのパスを引数に指定すると、
（例：　python wav_show.py interphone.wav）
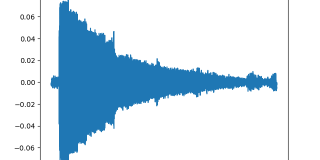
以下のようなグラフが表示されます。

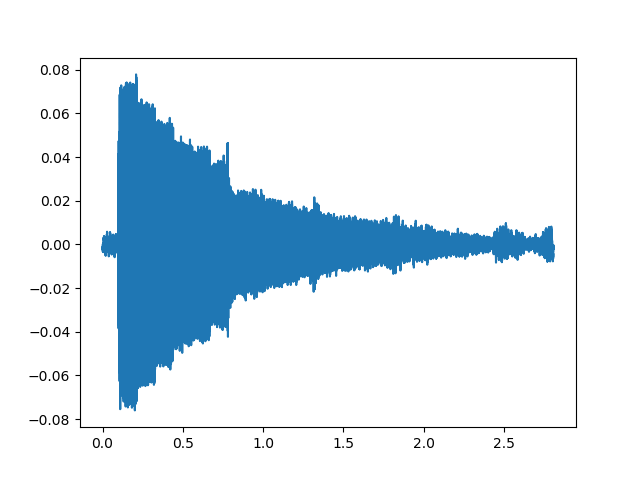
横軸が周波数、縦軸が振幅です。

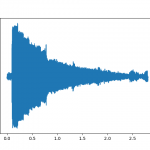
音声データが波になっていることを確認するために、このグラフを拡大し、最初の1000サンプルのデータを見てみます。

import sys
import scipy.io.wavfile
import numpy as np
import matplotlib.pyplot as plt


#音声ファイル読み込み
args = sys.argv
wav_filename = args[1]
rate, data = scipy.io.wavfile.read(wav_filename)

##### 音声データをそのまま表示する #####
#縦軸（振幅）の配列を作成
data = data / 32768
#横軸（時間）の配列を作成　　#np.arange(初項, 等差数列の終点, 等差)
time = np.arange(0, data.shape[0]/rate, 1/rate)  
#データプロット
plt.plot(time, data)
plt.xlim(0, 1000/rate)
plt.show()

データプロットのところに
plt.xlim(0, 1000/rate)
を加えただけです。

　　　

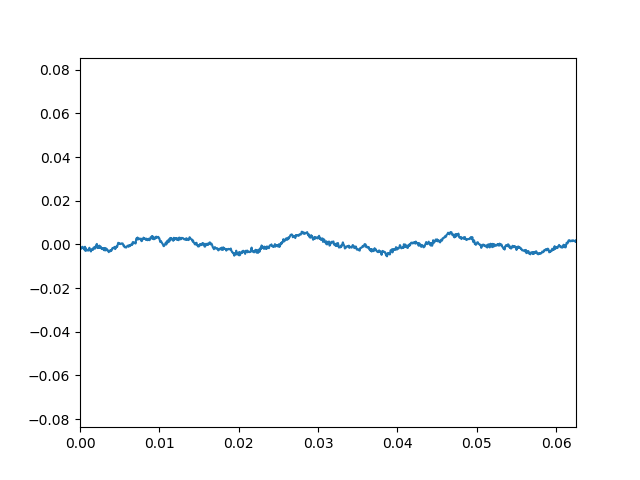
周波数成分を表示

続いて、フーリエ変換を用いてこの音声データの周波数成分を求めてみます。

import sys
import scipy.io.wavfile
import numpy as np
import matplotlib.pyplot as plt


#音声ファイル読み込み
args = sys.argv
wav_filename = args[1]
rate, data = scipy.io.wavfile.read(wav_filename)


#（振幅）の配列を作成
data = data / 32768

##### 周波数成分を表示する #####
#縦軸：dataを高速フーリエ変換する（時間領域から周波数領域に変換する）
fft_data = np.abs(np.fft.fft(data))    
#横軸：周波数の取得　　#np.fft.fftfreq(データ点数, サンプリング周期)
freqList = np.fft.fftfreq(data.shape[0], d=1.0/rate)  
#データプロット
plt.plot(freqList, fft_data)
plt.xlim(0, 8000) #0～8000Hzまで表示
plt.show()

先ほどと同様に音声ファイルを指定してこのプログラムを実行してみると、以下のようなグラフが表示されます。

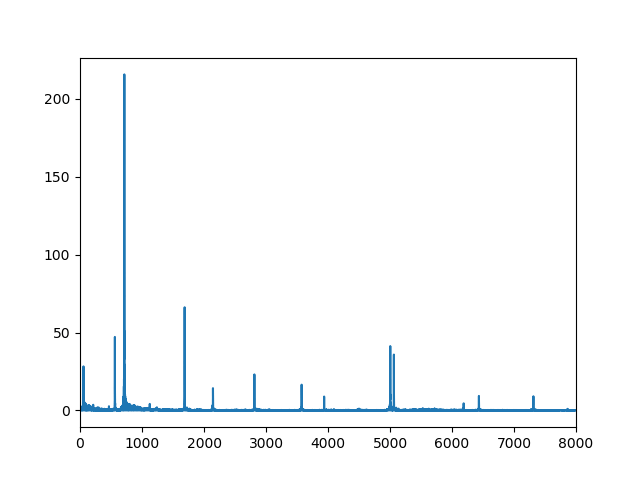
横軸が周波数、縦軸が振幅です。

このグラフをもとに、チャイムの”ピーンポーン”の周波数を調べてみたところ、おそらくグラフの最も大きいピーク(725Hz付近)が”ピーン”で、三番目に大きいピーク(560Hz付近)が”ポーン”であるとわかりました。

↓元の音

↓ピーンの部分（ 725Hzのサイン波 ）

↓ポーンの部分（ 560Hzのサイン波 ）

　　　

スペクトログラムを表示

高速フーリエ変換では音声データを時間領域から周波数領域に変換するだけなので、どの時間にどのような周波数が含まれているのか、というようなことがわかりません。

そこで 、フーリエ変換を短時間ごとに区切って行う（短時間フーリエ変換(STFT)）ことで、その短時間にどのような周波数が含まれているのかを調べることができます。

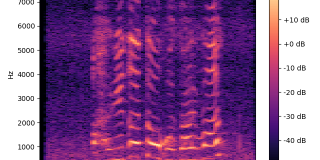
スペクトログラムとは、これをグラフ化した以下のようなグラフのことで、どの時間にどのような周波数がどれくらい含まれているのかがわかります。

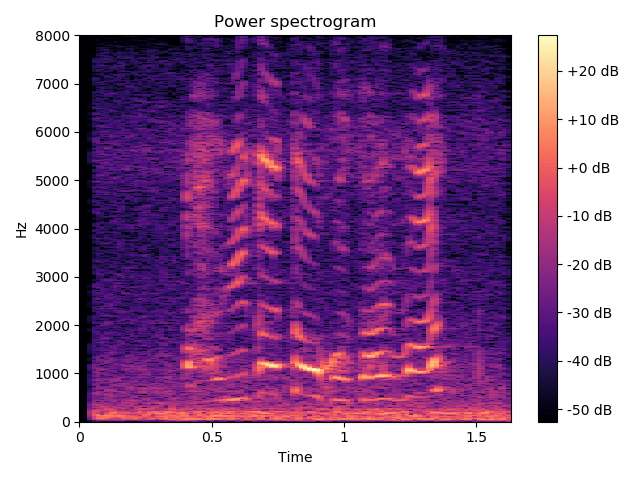
以下のプログラムを実行すると、このスペクトログラムを表示することができます。

import sys
import numpy as np
import librosa
import matplotlib.pyplot as plt
import scipy.io.wavfile
import librosa.display


#音声ファイル読み込み
args = sys.argv
wav_filename = args[1]
rate, data = scipy.io.wavfile.read(wav_filename)

#16bitの音声ファイルのデータを-1から1に正規化
data = data / 32768
# フレーム長
fft_size = 1024                 
# フレームシフト長 
hop_length = int(fft_size / 4)  


# 短時間フーリエ変換実行
amplitude = np.abs(librosa.core.stft(data, n_fft=fft_size, hop_length=hop_length))

# 振幅をデシベル単位に変換
log_power = librosa.core.amplitude_to_db(amplitude)

# グラフ表示
librosa.display.specshow(log_power, sr=rate, hop_length=hop_length, x_axis='time', y_axis='hz', cmap='magma')
plt.colorbar(format='%+2.0f dB')  
plt.show()                        

先ほどと同様に音声ファイルを指定してこのプログラムを実行してみると、以下のようなグラフが表示されます。

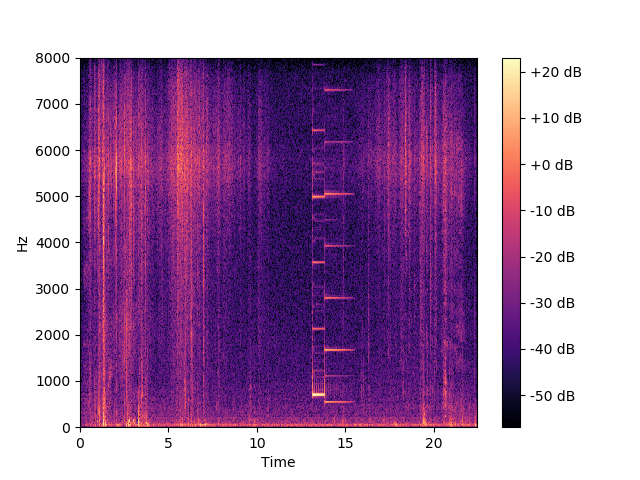
13秒あたりから16秒くらいにかけてインターホンが鳴っていることがわかります。

また、先ほどの周波数成分と比較してみると、当然ですが同じ周波数のところにピークが確認できます。

　　

追記(エラーが出る場合の解決法)

上記のスペクトログラムを表示するプログラムはモノラル音声にのみ対応しており、ステレオのwavファイルを読み込んで実行しようとすると、

~\.conda\envs\noise_cansel\lib\site-packages\librosa\util\utils.py in valid_audio(y, mono)
    293         raise ParameterError(
    294             "Invalid shape for monophonic audio: "
--> 295             "ndim={:d}, shape={}".format(y.ndim, y.shape)
    296         )
    297 

ParameterError: Invalid shape for monophonic audio: ndim=2, shape=(44927, 2)

といったようなエラーが表示されてしまいます。

モノラルとはチャンネル数が1の音声データで、ステレオとはチャンネル数が2の音声データのことを指します。

使用しようとしている音声ファイルがモノラルなのかステレオなのかを調べたい場合は以下のプログラムを実行してみてください。

import wave

wf = wave.open("/path/to/ファイル名.wav", "r")
print("チャンネル数：{}".format(wf.getnchannels()))

このプログラムを実行して、チャンネル数：2と表示された場合はステレオ音声なので、以下の記事を参考にしてモノラルに変換してからもう一度実行してみてください。

pythonで音声ファイルをモノラル・ステレオ変換する方法

また、上記の記事でmp3からwavに変換するプログラムも紹介しているので、wavファイルではなくmp3ファイルの解析をしたい方も参考にしてみてください。

　　　　

まとめ

今回は、フーリエ変換を用いて音声データの周波数成分を解析しました。解析して表示させたグラフは元データ、周波数成分、スペクトログラムの3つのグラフだけですが、これらの解析で得られたデータを利用すれば、音声認識プログラムなどを作成することができます。

次回は今回解析したデータをもとに、インターホンのチャイムを感知し、ラインを通知するプログラムを作成する方法について記載しようと思います。

　　　

参考サイト

・https://www.creativ.xyz/pysound-5-865